Wondershare AllMyMusic 2.4.2 | Mac OS X | 12 MB.
Dec 20, 2019 Wondershare AllMyMusic 3.0.1 - High-quality recorder for streaming audio. Download the latest versions of the best Mac apps at safe and trusted MacUpdate.
  • Shop Kingspan Insulation R-3 0.56-in x 4-ft x 8-ft 1 Unfaced Polystyrene Foam Board Insulation in the Foam Board Insulation department at Lowe's.com. For use as general purpose insulation for roofing, wall and foundation applications.
  • Eigenvalues and Eigenvectors of a 3 by 3 matrix Just as 2 by 2 matrices can represent transformations of the plane, 3 by 3 matrices can represent transformations of 3D space.
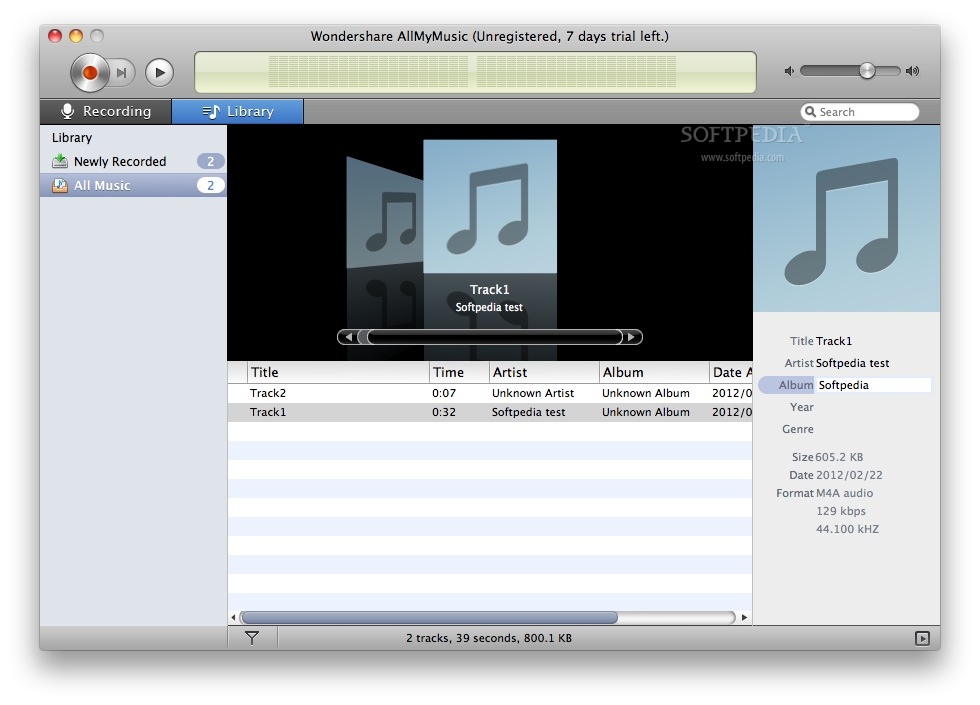
Record audio from any source of transmission, including web videos, radio stations, popular Web sites like YouTube, Pandora and more.

An unlimited supply of free music just a click

Want to listen to your songs, radio programs and audio favorite video at any time without Internet connection? It effortlessly burn them with professional Mac audio recorder. AllMyMusic for Mac Wondershare recorder is a high – quality audio for Mac that lets you record music and online radio programs with quality 1: 1 with one click. AllMyMusic for Mac meets all legislation on copyright and their use is 100% legal.
Note: This software is compatible with Mac OS X 10.8 without the functional problem.

Automatically detects the media being played

Open your Internet browser and access audio playback you want to record. Now, press the Record button (Record) without leaving the page and click the “Play (Play)” button on the search engine and you get the job done. As the Audio Recorder for Mac uses a virtual sound card to record any audio that is playing through the sound card on your computer, keeps 100% of the original audio quality.

Do not expect quality loss

Allmymusic
Whatever it is, as long as you can hear online, you can record quality 1: 1 Mac Audio Recorder. Free to use on the fly without worrying about waiting for the endless buffering, Audio Recorder for Mac OS X helps you break free Internet lace. Moreover, even divided automatically track while recording advertising and filters ensuring a great playback experience.

Get intelligently about music

When you start an audio recording, AllMyMusic for Mac can get the details of the recording artist, album, and genre automatically. You can also edit each label to make a playlist in style.

Tested and proven on the main pages

Wondershare AllMyMusic for Mac has been tested to record smooth-quality 1: 1 in more than 500 radio stations and pages of online music, including many famous playback pages as listed below: YouTube, Pandora, Napster, Spotify, Guba , NPC, MySpace, archive.org, BBC Radio Audio, iTunes Radio, RTVE, Sirius Radio, Radio Blog Club, XM Radio Online, AOL Music, etc.

To find a missing number in a Sequence, first we must have a Rule Airflow 2 4 1.

Sequence

A Sequence is a set of things (usually numbers) that are in order.
Each number in the sequence is called a term (or sometimes 'element' or 'member'), read Sequences and Series for a more in-depth discussion.

Finding Missing Numbers

To find a missing number, first find a Rule behind the Sequence.
Sometimes we can just look at the numbers and see a pattern:

Example: 1, 4, 9, 16, ?

Answer: they are Squares (12=1, 22=4, 32=9, 42=16, ..)

Rule: xn = n2

Sequence: 1, 4, 9, 16, 25, 36, 49, ..
Did you see how we wrote that rule using 'x' and 'n' ?
Allmymusic

xn means 'term number n', so term 3 is written x3

And we can calculate term 3 using:

x3 = 32 = 9

We can use a Rule to find any term. For example, the 25th term can be found by 'plugging in' 25 wherever n is.

x25 = 252 = 625

How about another example:

Example: 3, 5, 8, 13, 21, ?

After 3 and 5 all the rest are the sum of the two numbers before,
That is 3 + 5 = 8, 5 + 8 = 13 etc, which is part of the Fibonacci Sequence:
3, 5, 8, 13, 21, 34, 55, 89, ..
Which has this Rule:

Rule: xn = xn-1 + xn-2

Now what does xn-1 mean? It means 'the previous term' as term number n-1 is 1 less than term number n.
And xn-2 means the term before that one.
Let's try that Rule for the 6th term:

x6 = x6-1 + x6-2

x6 = x5 + x4

So term 6 equals term 5 plus term 4. We already know term 5 is 21 and term 4 is 13, so:

x6 = 21 + 13 = 34

Many Rules

One of the troubles with finding 'the next number' in a sequence is that mathematics is so powerful we can find more than one Rule that works.

What is the next number in the sequence 1, 2, 4, 7, ?

Here are three solutions (there can be more!):

Solution 1: Add 1, then add 2, 3, 4, ..
So, 1+1=2, 2+2=4, 4+3=7, 7+4=11, etc..
Rule: xn = n(n-1)/2 + 1 Bettertouchtool 2 312 – customize multi touch trackpad gestures free.
Sequence: 1, 2, 4, 7, 11, 16, 22, ..
(That rule looks a bit complicated, but it works)
Solution 2: After 1 and 2, add the two previous numbers, plus 1:
Rule: xn = xn-1 + xn-2 + 1
Sequence: 1, 2, 4, 7, 12, 20, 33, ..
Solution 3: After 1, 2 and 4, add the three previous numbers
Rule: xn = xn-1 + xn-2 + xn-3
Sequence: 1, 2, 4, 7, 13, 24, 44, ..
So, we have three perfectly reasonable solutions, and they create totally different sequences.

Allmymusic 3 0 1 5 X 4 5

Which is right? They are all right. And there are other solutions ..

.. it may be a list of the winners' numbers .. so the next number could be .. anything!

Simplest Rule

When in doubt choose the simplest rule that makes sense, but also mention that there are other solutions.

Finding Differences

Sometimes it helps to find the differences between each pair of numbers .. this can often reveal an underlying pattern.
Here is a simple case:
The differences are always 2, so we can guess that '2n' is part of the answer.
Let us try 2n: Navicat premium 11 1 8 download free.
The last row shows that we are always wrong by 5, so just add 5 and we are done:

Rule: xn = 2n + 5

OK, we could have worked out '2n+5' by just playing around with the numbers a bit, but we want a systematic way to do it, for when the sequences get more complicated.

Second Differences

In the sequence {1, 2, 4, 7, 11, 16, 22, ..} we need to find the differences ..
.. and then find the differences of those (called second differences), like this:
The second differences in this case are 1.

Allmymusic 3 0 1 5 X 4 5 Picture Frame

With second differences we multiply by n22

In our case the difference is 1, so let us try just n22:
n:12345
Terms (xn):124711
n22:0.524.5812.5
Wrong by:0.50-0.5-1-1.5
We are close, but seem to be drifting by 0.5, so let us try: n22 − n2
Wrong by 1 now, so let us add 1:

Allmymusic 3 0 1 5 X 4 X 8 Foam Insulation Sheets

n22 − n2 + 1124711
Wrong by:00000
We did it!
The formula n22 − n2 + 1 can be simplified to n(n-1)/2 + 1
So by 'trial-and-error' we discovered a rule that works:

0 Divided By 1

Rule: xn = n(n-1)/2 + 1

Sequence: 1, 2, 4, 7, 11, 16, 22, 29, 37, ..

Other Types of Sequences

Read Sequences and Series to learn about:
And there are also:
And many more!
In truth there are too many types of sequences to mention here, but if there is a special one you would like me to add just let me know.